| > | # DU: fibonacciho metoda, vstup,počet kroků, výsledkem bude animace grafu, v každým kroku bude vidět, jak se zmenšuje interval. Subj emailu: INNMO ukol |
| > | restart; |
| > | f:=x->(x^2); |
| (1) |
| > | with(plots):
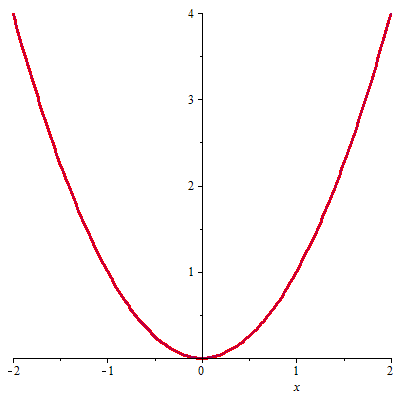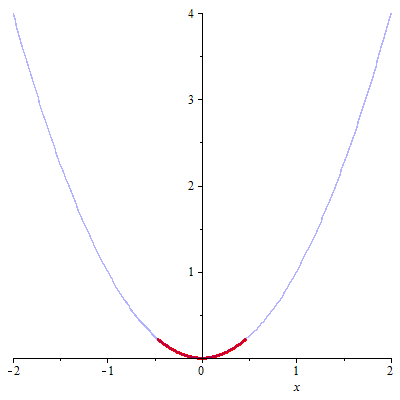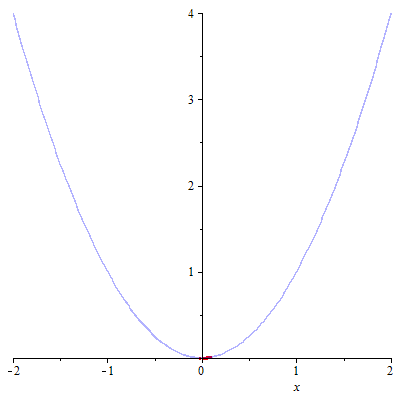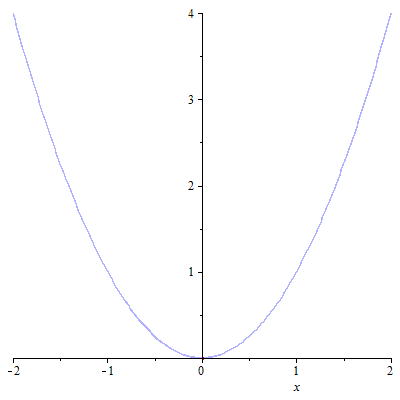
with(combinat,fibonacci): fibonacciNalezeniMinima:=proc(fce,a,b,kroku) local k, xk1, xk2, ak:=a, bk:=b, castecna, cela, N:=kroku+1; xk1:=evalf(bk-((fibonacci(N-1)/fibonacci(N))*(bk-ak))); xk2:=evalf(ak+((fibonacci(N-1)/fibonacci(N))*(bk-ak))); # printf("xk1: %f, xk2: %f",xk1,xk2); cela:=plot(fce(x),x=a..b,color=blue,transparency=0.7,thickness=1); castecna[0]:=plot(fce(x),x=a..b,color=red,transparency=0,thickness=3); for k from 1 to N-1 do if (evalf(fce(xk1)) <= evalf(fce(xk2))) then ak:=ak; bk:=xk2; xk2:=evalf(xk1); xk1:=evalf(bk-(fibonacci(N-k)/fibonacci(N-k+1))*(bk-ak)); else ak:=xk1; bk:=bk; xk1:=evalf(xk2); xk2:=evalf(ak+(fibonacci(N-k)/fibonacci(N-k+1))*(bk-ak)); end if; castecna[k]:=plot(fce(x),x=ak..bk, color=red,transparency=0,thickness = 3); end do; printf("Iterací provedených: %a\r",N-1); printf("Nalezené minimum: %f ",(ak+bk)/2); display(display(seq(castecna[t],t=0..N-1),insequence=true),cela); end proc: |
| > | fibonacciNalezeniMinima(f,-2,2,10); |
| Iterací provedených: 10 Nalezené minimum: 0.013653 | |
 |
| > |